Simulated Knitting

Alternate title: I'm a big fan of the Fruchterman & Reingold graph embedding algorithm.


Recently I created a site for trying to predict the pattern of colors in pooled knitting.

Next I wanted to be able to predict the shape of a knitted object. I'll explain more in a minute, but first here are some examples (click on the images for a gif movie):

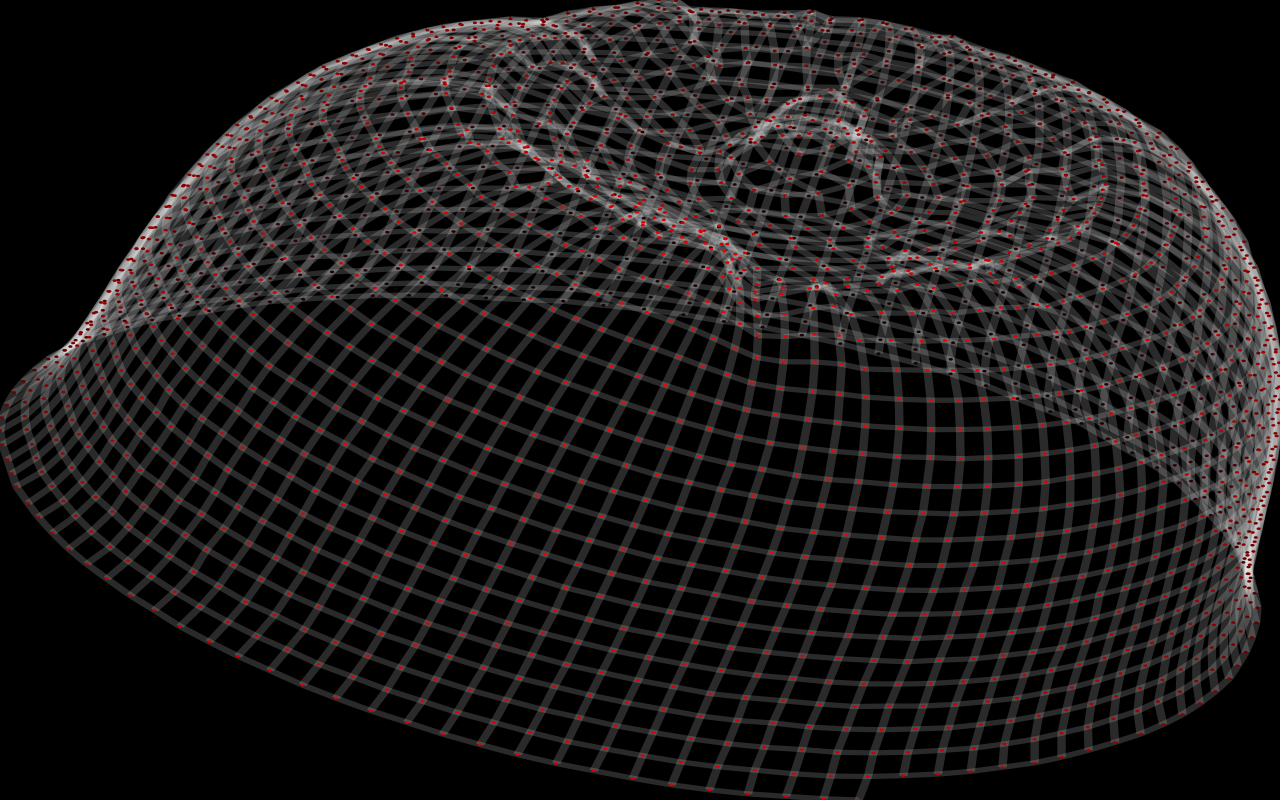
A hat:

Some flat knitting (doesn't look flat to you? I'll explain in a minute):

So, what's going on here? I've done two things:

1.  Construct an abstract graph corresponding to something someone might knit
2. Embed that graph in 3D (determine where each of the points of the graph should go)

The tricky part is (2), although, as you'll see, I didn't do any of the work on that myself. I was thinking that I should approach the embedding by simulating each vertex as acted on by two forces:

• Attractive:  Applies to each pair of vertices connected by an edge, tries to pull them close to each other like a spring.
• Repulsive: Applies to each pair of vertices (regardless of whether they are connected by an edge), pushes them apart. Primarily a close-range force, infinitely strong in the limit as the points get very close together.

As it turns out, this is a very popular algorithm from Fruchterman & Reingold for graph embeddings (already implemented in iGraph). The classic paper is all about embeddings in 2D, but there's no reason not to do this in 3D. In their algorithm, the attractive force increases as distance^2 (unlike springs), and the repulsive force increases as (1/distance).

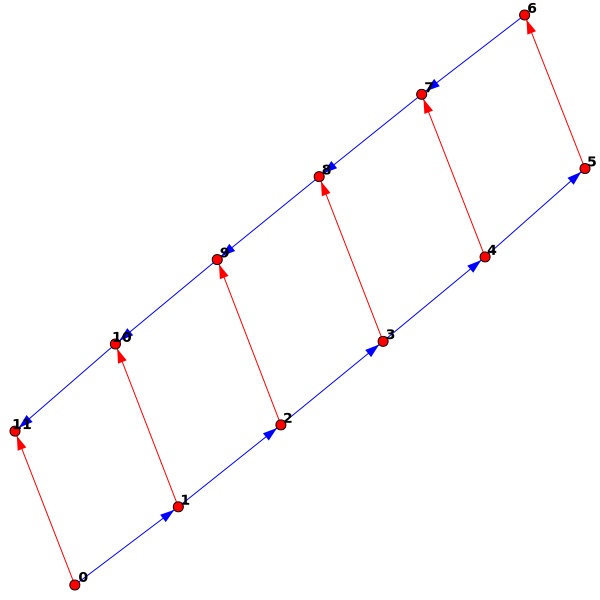
So, I just have to construct graphs that correspond to things you might knit. To illustrate the idea, here's a very simple example:


And the code (after I wrote the appropriate methods) to generate it:

g = KnittedGraph()  #Create new "KnittedGraph" object
g.AddStitches(5)    #Add five stitches
g.NewRow()          #Create a new row
g.FinishRow()       #Finish the new row

This creates the graph, adds five stitches, starts a new row, and then finishes that row. The "flat knitting" above was created just like this: "cast on" 50 stitches, and then knit 20 rows back and forth. Why didn't it lie flat, though? The real answer: Forcing it to lie flat isn't what would make sense! The real knitting (just like a real "flat") piece of paper has the option to bend in one direction at a time. The algorithm has a certain distance apart that it wants each pair of linked vertices to be, and the object doesn't have to lie flat to achieve that.

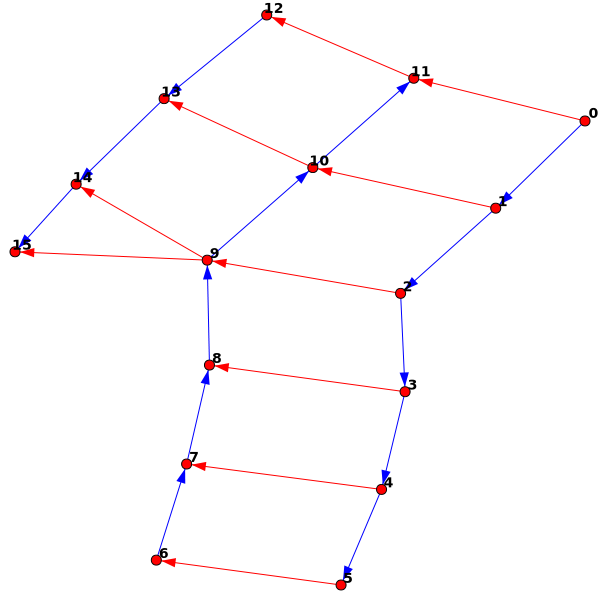
Extending this a little, I can add an "increase" (two stitches connected to the same stitch in the previous row):

g = KnittedGraph()  #Create new "KnittedGraph" object
g.AddStitches(5)    #Add five stitches
g.NewRow()          #Create a new row
g.FinishRow()       #Finish the new row
g.NewRow()       
g.AddStitch()
g.Increase()        #Add an "increase" (one stitch connected to two in the previous row)

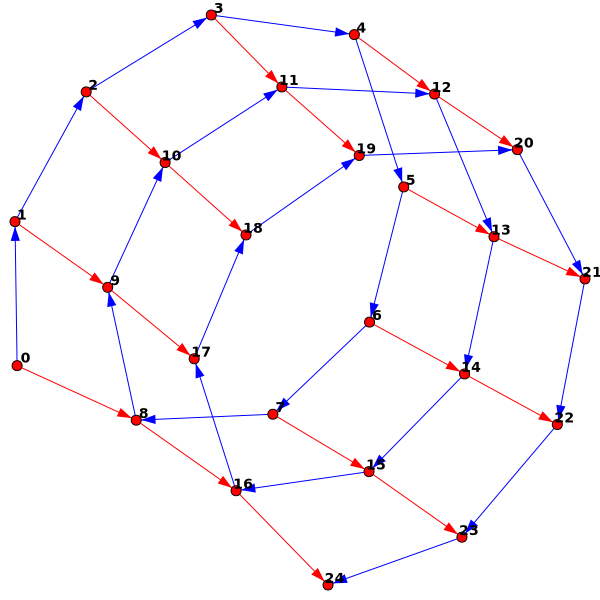
We can also knit "in the round" by knitting a row and then connecting the current stitch to the first stitch:

g = KnittedGraph()
g.AddStitches(8)
g.ConnectToZero() #Connect the current stitch to the original stitch
g.AddStitches(16) #Knit two more rows (by adding 16 stitches)

Here's an example of the same thing (but larger -- 20 circular rows of 50 stitches each) embedded in 3d:

As a final example, let's try to make something with constant negative curvature (a pseudo-sphere).  Geeky knitters often do this for fun by knitting in a circle (as above) and increasing the number of stitches at a constant rate:

The way I like to think about this mathematically, negative curvature for a surface means that small discs of a given radius have more volume than on a flat plane (and the opposite for positive curvature). Think of squashing a saddle flat and having extra material, vs. squashing a hemisphere flat and not having enough.

And here's mine:

Here's my code on GitHub.

(Including a modified version of this code for plotting in 3D.  Thanks Michael!)

[Edit: Using Ubuntu 10.04.3 LTS & Python 2.6.5, I installed python-iGraph with:  
sudo aptitude install python-igraph



Apparently that's not working in Ubuntu 11.10. See this G+ thread for more. Thanks, Shae.]